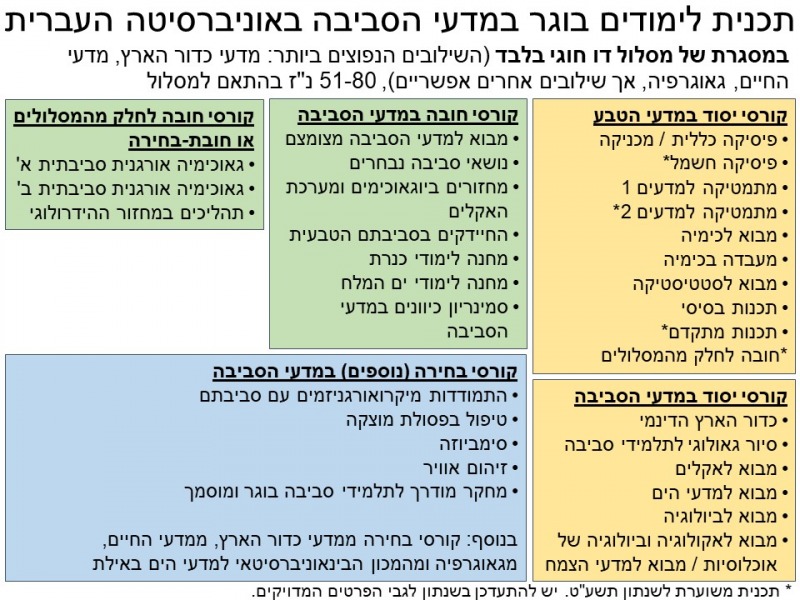
הלימודים לבוגר מוצעים בהיקף של חוג רגיל. תוכלו ללמוד בתכנית רק במסלול דו-חוגי, בשילוב עם חוג אחר (ראו שנתון האוניברסיטה). אנו ממליצים על שילוב של מדעי הסביבה עם מדעי כדור הארץ או עם מדעי החיים, אך ניתן גם לשלב עם החוגים כימיה, פיסיקה ומדעי המחשב. כמו כן, ניתן לשלב גם עם אחד מהחוגים הבאים מפקולטות אחרות באוניברסיטה: תקשורת ועיתונאות, גאוגרפיה, חינוך, יחסים בין-לאומיים, מדע המדינה, כלכלה, סטטיסטיקה, מנהל עסקים, חשבונאות, סוציולוגיה ואנתרופולוגיה, פסיכולוגיה, פילוסופיה, היסטוריה של עם ישראל, ארכאולוגיה או משפטים. השילוב עם פקולטות אחרות קשה יותר, ומומלץ רק לסטודנטים מצטיינים.
במהלך התואר תרכשו ידע יסודי במדעי הטבע (פיסיקה, כימיה, מתמטיקה), תלמדו קורסי מבוא במדעי הסביבה, ותקבלו בסיס רחב וחזק במדעי החיים ובמדעי כדור הארץ. בשנים מתקדמות לתואר יקשרו קורסים ייחודיים לחוג למדעי הסביבה בין התחומים המדעיים שנלמדו לאתגרי הסביבה.

